01. 배열
그동안 우리는 많은 데이터를 저장하기 위해 주로 배열을 사용했습니다. 이후에는 배열이 아닌 수많은 자료구조에 대해 학습하겠지만, 일단 배열의 특성을 이해하고 어떤 장점과 단점이 있는지 알아봅시다.
우리는 배열로 무엇을 하나요? 주로 값을 담고, 값을 배열에서 삭제하고, 원하는 값을 배열에서 찾습니다.
이런 삽입, 삭제, 탐색 연산을 일반적으로 기본 연산이라고 부릅니다. 각각의 시간복잡도를 생각해봅시다.
삽입
실제로는 값을 어디에 삽입하냐에 따라 시간복잡도는 달라집니다. 다만, 보통 시간복잡도라 부를 때에는 최악의 상황에서의 시간복잡도를 얘기합니다.
배열이 주어졌을 때, 앞이나 가운데에 값을 넣는다고 가정합시다. 이렇게 되면 다음과 같이 새로운 값이 들어갈 자리를 확보하기 위해 다른 값들이 한칸씩 이동해야 합니다. 따라서 일반적으로 삽입의 시간복잡도는 이 됩니다.
다만, 항상 배열의 맨 뒤에 새로운 값을 삽입하는 경우만 발생한다면, 이런 경우엔 다른 값들의 이동이 전혀 존재하지 않기 때문에 의 시간복잡도를 보일 것입니다.

삭제
삽입과 마찬가지로, 맨 뒤의 값을 제거하게 된다면 이 걸릴 것입니다. 그러나 삭제의 주 목적은 우리가 원하는 값을 지우는 것이기 때문에, 맨 뒤의 값이 아닌 다른 값을 제거하는 경우도 살펴봐야 할 것입니다. 이런 경우엔, 삽입 과정에서 설명했던 것과 유사하게 다른 값들의 이동이 따라옵니다.
최악의 경우, 맨 앞의 값을 삭제하게 된다면 나머지 N-1개의 값들이 모두 이동해야 하기 때문에 의 시간복잡도를 보일 것입니다.
탐색
원하는 값을 찾으려면 어떤 방법이 있을까요? 가장 간단한 방법은 바로 처음부터 모든 값을 훑는 것입니다.
당연히 맨 끝에 값이 존재한다면 모든 값을 탐색해야 할 겁니다. 그렇게 된다면 자연스럽게 탐색의 시간복잡도도 마찬가지로 이라고 볼 수 있을 겁니다.
k번째 원소 값 구하기
배열이 주어졌을 때, k번째 원소를 찾는 데 걸리는 시간은 어떻게 될까요?
배열은 index 기반으로 이루어져 있기 때문에 k - 1번째 index를 참조하면 바로 k번째 원소를 구할 수 있습니다. 따라서 이 경우의 시간복잡도는 O(1)이 됩니다.
>> 문제 풀이
1. arr.find(i) 의 시간 복잡도는 O(N)
이 과정을 모든 i에 대해 arr.size()번; 즉 n번 실행되게 되므로, 전체 for 문의 총 시간 복잡도는 O(N^2)이다.
2.


6번 문제 : k번째 원소 값을 구하기 위한 시간 복잡도는 O(N)이 될 것 이다. (x)
02. 동적 배열
C++에서 배열을 선언하기 위해서는 다음과 같이 선언했었습니다.
int a[100];
이렇게 선언하여 만들어지는 배열을 정적 배열이라고 부릅니다. 정적 배열의 경우에는 배열의 선언과 동시에 그 크기를 정해줘야 하며, 한번 선언된 이후부터는 크기를 바꿀 수 없습니다. 하지만 자주 길이가 바뀌는 경우라면, 명확히 메모리를 낭비하고 있는 것이 아닐까요? 이러한 문제를 해결하기 위해 나온 것이 바로 동적 배열입니다.
동적 배열은 자유롭게 길이가 줄어들고 늘어날 수 있습니다. 즉, 정확히 사용하고 싶은 만큼만 공간을 차지하여 사용하는 방식입니다.

동적 배열에서 삽입, 삭제, 탐색하는 과정은 모두 정적 배열과 동일하기 때문에 시간복잡도는 완전히 일치하지만, 메모리를 필요한 만큼만 사용한다는 차이가 있습니다.
C++에서는 동적 배열을 vector를 이용하여 표현할 수 있습니다.
vector를 사용하기 위해서는 #include <vector> 헤더와, vector<T> name; 형태의 선언이 필요합니다. T는 타입으로, 벡터 안에 들어갈 원소의 타입을 적어줘야 합니다.
또, vector는 원래 std::vector로 쓰여야 하므로 using namespace std;를 미리 적어 vector 만으로도 이용이 가능하도록 하는 것이 좋습니다.
정수를 관리할 벡터는 다음과 같이 선언해 볼 수 있습니다.
#include <iostream>
#include <vector>
using namespace std;
int main() {
vector<int> v;
return 0;
}
vector를 이용할 때 자주 사용되는 것은 다음 4가지 입니다.
- push_back(E) : 맨 뒤에 데이터 E를 추가합니다.
- pop_back() : 맨 뒤에 있던 데이터를 하나 삭제합니다.
- size() : 현재 vector에 들어있는 데이터의 수를 반환합니다.
- index로 데이터 조회 : 배열과 마찬가지로, index를 통해 데이터를 조회합니다.
따라서 다음과 같이 코드를 작성해볼 수 있습니다.
#include <iostream>
#include <vector>
using namespace std;
int main() {
vector<int> v; // 정수를 관리할 벡터를 선언하고 => 빈 벡터
v.push_back(5); // v : [5]
cout << v.size() << endl; // 들어있는 데이터의 수 : 1개
cout << v[0] << endl; // 0번지에 들어 있는 값 : 5
v.push_back(2); // v : [5, 2]
v.push_back(9); // v : [5, 2, 9]
cout << v[1] << endl; // 1번지에 들어 있는 값 : 2
cout << v[2] << endl; // 2번지에 들어 있는 값 : 9
cout << v[3] << endl; // 3번지에 들어 있는 값 : 존재하지 않으므로 Error 발생
// 현재 벡터 내에 있는 모든 데이터를 순회하기 위해서는
// 데이터의 개수인 v.size()를 활용하여
// 포문을 통해 순회가 가능합니다.
for(int i = 0; i < v.size(); i++)
cout << v[i] << endl; // 출력 결과 : 순서대로 5 2 9
v.pop_back(); // 맨 뒤에 있는 원소를 제거합니다.
cout << v.size() << endl; // 들어있는 데이터의 수 : 2개
for(int i = 0; i < v.size(); i++)
cout << v[i] << endl; // 출력 결과 : 순서대로 5 2
return 0;
}
Side Note
C++에서는 vector 뿐만이 아니라 stack, queue, deque 등의 자료구조들을 사용할 수 있습니다. 이렇게 사용이 가능한 이유는 C++에서 이런 자료구조를 사용할 수 있도록 미리 STL(표준 템플릿 라이브러리)를 만들어 놓았기 때문입니다. 이렇게 STL로 정의되어 있는 자료구조들을 컨테이너라고 부릅니다. vector, stack 등이 바로 컨테이너 입니다. 이러한 컨테이너 내에 있는 원소들을 순회하는 위해 iterator라는 이름의 반복자를 사용하기도 합니다.
iterator는 다음과 같은 형태로 정의되어야 합니다.
(기존 컨테이너 type) ::iterator it;
즉 숫자를 담는 vector 컨테이너를 조회하기 위한 iterator는 다음과 같이 정의가 됩니다.
vector<int>::iteator it;
iterator를 이용하여 vector를 순회하기 위해서는 시작과 끝을 알아야 하는데, 시작 원소를 나타내는 위치는 v.begin(), 마지막 원소 그 다음 위치는 v.end()로 구해집니다.
여기서 v.end()가 마지막 원소가 아닌, 마지막 원소 그 다음 위치인 이유는 아래 코드를 보면 이해해볼 수 있습니다.
#include <iostream>
#include <vector>
using namespace std;
int main() {
vector<int> v; // 정수를 관리할 벡터를 선언하고 => 빈 벡터
v.push_back(5); // v : [5]
v.push_back(2); // v : [5, 2]
v.push_back(9); // v : [5, 2, 9]
// Iterator를 이용한 Vector 컨테이너 내의 원소들 순회
vector<int>::iterator it;
for(it = v.begin(); it != v.end(); it++) { // 5 2 9
cout << *it << endl; // it가 가리키는 주소에 담긴 데이터 참조를 위해 * 사용
}
return 0;
}
위의 코드에서 for문을 보면, it는 원소가 처음 들어있는 위치인 v.begin()에서 시작하여, v.end()가 되기 전까지 한 칸씩 전진하며 for문을 진행합니다.
즉, v.end()가 마지막 데이터 그 다음 위치이기 때문에 for문에서 it가 v.end()가 되는 순간 종료해주는 것으로 깔끔하게 코드 구현이 가능합니다. iterator는 마치 pointer와 같이 때문에 각 원소의 주소를 계속 가리키게 되고, 해당 주소에 담겨있는 데이터를 참조하기 위해서는 pointer에서 값을 참조하는 것 처럼 앞에 *을 꼭 붙여줘야 합니다.
따라서 코드에서는 원소를 출력하기 위해 *it값을 적어주었습니다.
03. 단일 연결 리스트 - 노드의 정의
배열의 시간복잡도를 생각해보면, 중간 삽입과 삭제의 시간복잡도가 이라는 것을 알 수 있습니다.
과 의 효율은 하늘과 땅 차이입니다.
그렇기 때문에 삽입과 삭제를 매우 자주 해야 하는 상황이라면, 배열은 조금 비효율적일 것입니다.
이런 문제를 해결하기 위해 연결 리스트라는 새로운 자료구조가 등장합니다.
이 자료구조는 탐색은 느리지만, () 삽입과 삭제 연산은 매우 빠르기 때문에 (둘 모두 ) 삽입과 삭제가 잦은 상황에서 자주 사용됩니다.
우선 연결 리스트를 이해하기 위해선 노드라는 개념에 대해 이해해야 합니다.
새로운 용어라 많이 겁먹을수도 있겠지만, 간단하게 말하자면 '정보를 담는 하나의 창구'라고 생각하면 됩니다.
일반적으로 연결 리스트에서 하나의 노드는 데이터와 다른 노드로 이동하는 경로를 갖고 있습니다.
아직 연결 리스트에 대해 깊게 공부하지 않았지만, 연결 리스트는 여러개의 노드가 모여서 형성되는 구조라고 생각하면 될 것입니다.

노드에 대해 이해하셨다면, 본격적으로 연결 리스트에 대해 알아봅시다.
앞에서 설명하였듯이, 연결 리스트란 노드가 여러개 모여서 만들어지는 하나의 구조라고 설명하였습니다.
그렇다면 '단일'은 어떤 것을 의미할까요? 바로 연결 방향이 단방향이라는 이야기 입니다.
마치 일방통행 같은 구조라고 생각하면 될 것 같습니다.
단일 연결 리스트
: 삽입과 삭제에 최적화된 자료구조로, 앞에서 학습한 노드 간의 연속적인 관계로 구성된 자료구조
앞에서 노드는 데이터와 다른 노드의 참조를 갖고 있다고 배웠습니다. 그렇다면 단일 연결 리스트의 노드가 갖고 있는 다른 노드의 참조란 어떤 노드를 말하는 것 일까요?
정의를 잘 생각해보면 진행방향으로 이었을 때의 바로 옆 노드를 말하는 것일 겁니다.
즉, 단일 연결 리스트의 구조는 다음과 같다고 생각할 수 있습니다.

여기서 각 노드별로 data와 next값을 가지고 있는데, Data는 값을, Next는 그 다음 노드의 위치를 가리키는 역할을 합니다.
예를 들어 다음과 같이 값 3을 갖는 노드가 하나 있다고 생각해봅시다.
이때, 그 다음 노드가 없기 때문에 Next에는 기본적으로 null(비어있다는 뜻)이 들어있습니다.

이렇게 새로운 node를 만드는 것은 다음과 같이 수도코드로 나타내 볼 수 있습니다.
next 값에 별다른 값을 넣어주지 않으면, 기본으로 null이 됩니다.
set node1 = node(3)
이 코드는 다음과 같이 data가 없는 상태로 만든 뒤, 해당 노드에 값을 넣어주는 식으로 표현해볼 수도 있습니다.
set node1 = node()
node1.data = 3
이 노드 바로 뒤에, 값이 5인 노드를 추가적으로 만들어 연결지어 보겠습니다.
먼저 값이 5인 노드를 새로 만들어줍니다. 이름은 node2 입니다.

그 다음 node1 뒤에 node2를 매달아야 하므로, node1.next를 node2로 설정해줍니다.

이렇게 새로운 노드 node2를 만들어, node1 뒤에 연결하는 수도 코드는 다음과 같이 작성해볼 수 있습니다.
set node2 = node(5)
node1.next = node2
그렇다면 node1.next가 의미하는 것은 무엇일까요?
node1.next라는 것은 바로 node2 자체를 의미합니다.

따라서 다음 코드를 실행하면 node2의 값이 출력됩니다.
set node1 = node(3)
set node2 = node(5)
node1.next = node2
print(node2.data) # 5
print(node1.next.data) # 5
그러면 연결되어 있는 node1, node2를 다시 분리 시키기 위해서는 어떻게 해야할까요?
바로 node1.next 값에 null을 넣어주면 됩니다.
set node1 = node(3)
set node2 = node(5)
node1.next = node2
print(node1.next.data) # 5
node1.next = null # 두 관계를 끊어줍니다.
그러면 다음과 같이 다시 분리가 됩니다.

이렇게 next 값에 null을 넣어주는 것은 뒤에서 노드를 삭제할 때 이용을 하게되기 때문에, 꼭 기억해주세요.
지금까지는 단일 연결 리스트가 생성되는 과정에 대해서 알아봤습니다. 그러나 이런 형태로 끝내면 문제가 발생할 수 있습니다. 시작점을 찾을 수 없다는 것 입니다.
예를 들어, 리스트의 모든 값을 탐색해야 하는 상황이 발생했는데, 시작점을 알 수 없다면 우리는 모든 값을 탐색했는지 판단할 수 없습니다.

따라서 우리는 리스트의 첫번째 값의 위치를 반드시 명시해야하며, 우리는 이것을 head라고 호칭할 것입니다.

더불어, 종료되는 지점도 알고 있으면 좋을 것입니다. 종료지점을 명시해놓으면 탐색할 때 추가적인 처리 없이 현재 방문한 노드가 종료 지점인지 판단하는 과정만 거쳐서 탐색을 종료할 수 있을 것입니다.
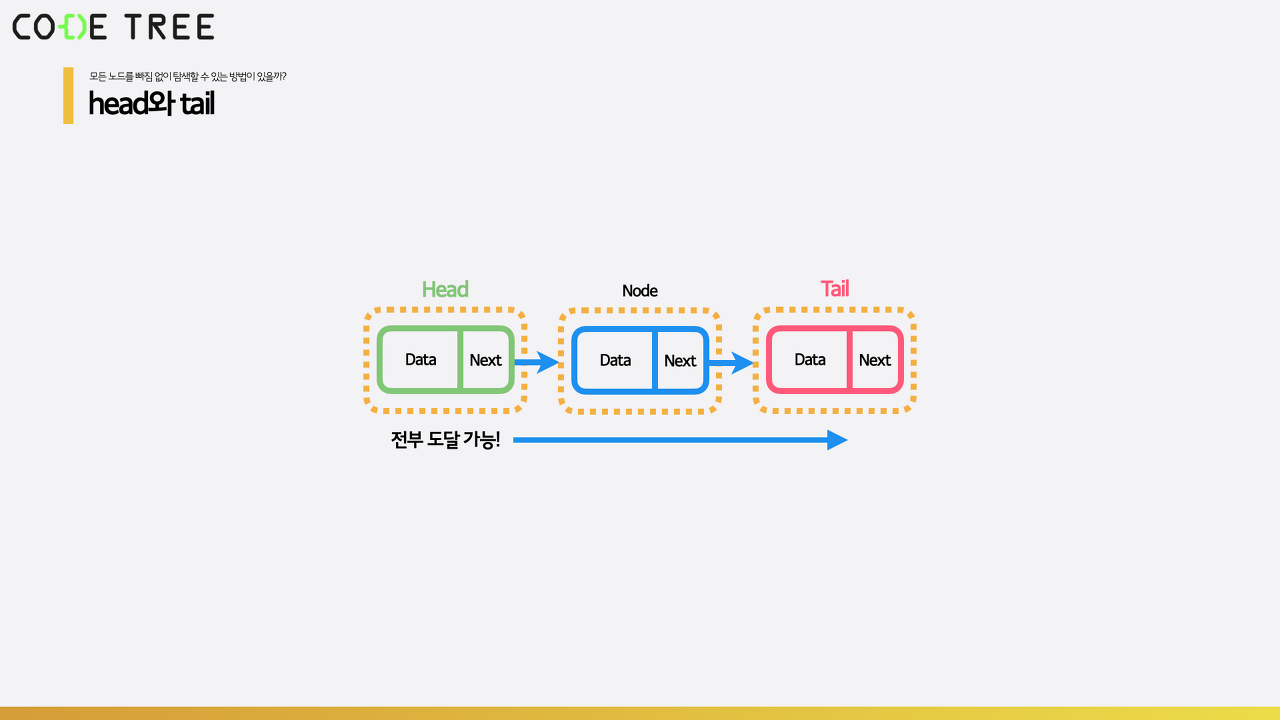
이처럼 단일 연결 리스트 역시 배열과 마찬가지로 삽입, 삭제, 탐색이 모두 가능한 자료구조 입니다.
- 이때 탐색은 Head부터 Tail까지 일일이 확인해야 하므로 이라는 시간이 소요됩니다.
- 하지만 단일 연결 리스트에서는 삽입, 삭제의 경우 인접한 곳의 선을 끊고 연결해주는 작업만 해주면 되므로 이라는 시간이 소요됩니다.
- 단, 일방향으로만 진행되기 때문에 뒤로 돌아갈 수 없는 구조임에 유의합니다.
<오답 노트>
1. 단일 연결 리스트에서 k번째 원소를 찾기 위해서는 반드시 head에서 출발하여 k번째 노드까지 가야함 > O(N)
2. 배열에서 k번째 원소를 찾기 위해서는 k-1번째 index 참고하면 되므로 >> O(1)이면 충분 O(N) X

04. 단일 연결 리스트 - 삽입/삭제/탐색
배열에서 했던 것 처럼, 연결 리스트에서도 삽입/삭제/탐색 연산을 수행해야 할 일이 있을 것입니다. 특히 앞에서 연결 리스트는 삽입과 삭제 연산에 최적화 된 자료구조라고 했으니, 어떤 방식으로 동작하는지 확실히 이해해야 할 것입니다.
삽입
tail 뒤쪽에 값을 삽입한다고 가정해봅시다. tail은 next가 비어있기 때문에, 새로운 노드가 들어오게 된다면 next가 가리키는 노드를 해당 노드로 지정해주면 연결 처리는 큰 문제 없이 될 것입니다. 그러나, 새로운 노드는 현재 tail보다 뒤쪽에 위치할 것이기 때문에, 추가적으로 tail이 가리키는 노드도 변경해줘야 합니다.

이 과정에 해당하는 코드는 다음과 같습니다.
function SLL.insert_end(num)
set new_node = node(num) # Step 1. 노드 만들기
SLL.tail.next = new_node # Step 2. 이어 붙이기
SLL.tail = new_node # Step 3. Tail 변경하기
비슷하게 접근하면, head 앞에 새로운 값을 추가하는 것도 문제 없이 구현할 수 있을 것입니다.

이 과정에 해당하는 코드는 다음과 같습니다.
function SLL.insert_front(num)
set new_node = node(num) # Step 1. 노드 만들기
new_node.next = SLL.head # Step 2. 이어 붙이기
SLL.head = new_node # Step 3. Head 변경하기
다만 head 바로 뒤에 노드를 추가하는 것은 조금 복잡합니다. 연결을 아무 생각 없이 끊어버리게 되면 예상치 못한 결과가 나올 수 있기 때문입니다.
따라서 다음 3가지 과정을 거쳐 진행합니다.
- 새로운 노드를 만들어 줍니다.
- 새로운 노드의 next 값을, head의 next값으로 설정해줍니다.
- head의 next 값을 새로운 노드로 변경합니다.



이렇게 3개의 과정을 거치게 되면, head 바로 뒤에 새로운 노드가 추가가 됩니다.
이 과정에 해당하는 코드는 다음과 같습니다.
function SLL.insert_after_head(num)
set new_node = node(num) # Step 1. 노드 만들기
new_node.next = SLL.head.next # Step 2. 새로운 노드의 next 값 변경
SLL.head.next = new_node # Step 3. Head의 next 값 변경
삭제
삽입과 유사하나, 삽입은 연결을 새로 정의하는 것과 반대로, 삭제는 연결을 제거해야 합니다.
삭제시 유의해야 할 점은, 삭제하게 되는 노드의 바로 전 노드에서 그 다음 노드로 연결관계를 바꿔줘야 한다는 것입니다.
예를 들어 tail을 삭제하는 과정은 다음과 같이 tail 바로 전 노드의 next 값을 먼저 null로 바꾼 뒤, tail을 그 전으로 옮겨주는 작업을 진행하면 됩니다.

그렇다면 head는 어떻게 삭제하면 될까요? 별로 어렵지 않습니다.
head의 값을 head.next로 지정하면 끝납니다. 실제로 값을 삭제하는 것은 아니지만, head.next로 정의하게 되면 우리가 참조하는 head 값은 그 다음 값이기 때문에, 노드가 정상적으로 삭제된 것 처럼 보일것입니다.

<오답>
function SLL.delete(num)
set node = SLL.head
while node.(1) != (2):
node = node.next
node.next = node.(3)

탐색
위에서 삽입하거나 삭제할 때 왜 굳이 head와 tail 까지 같이 옮겨줘야 할까요? 그 이유는 바로 탐색을 원활하게 하기 위함입니다.
단일 연결리스트에서 시작부터 끝을 확실히 정해줘야, 시작점에 해당하는 head부터 출발하여 tail이 나오기 전까지 계속 next를 따라가면서 탐색을 진행할 수 있기 때문입니다.

단, insert_front 함수는 head 앞에 노드를 추가하는 함수이고, insert_end는 tail 뒤에 노드를 추가하는 함수이며, delete_front 함수는 head를 제거하는 함수입니다.
<문제>
- 연결 리스트 합치기
오름차순으로 정렬된 두 연결 리스트가 있습니다. 우리의 목표는 두 연결 리스트를 하나로 합치되, 합쳐진 결과물도 정렬 되도록 하는 것입니다.
function solution(SLL1, SLL2)
set result = empty SLL
node1 = SLL1.head
node2 = SLL2.head
while node1 != null or node2 != null
if node2 == null or (1)
result.insert_end((2))
node1 = node1.next
else
result.insert_end((3))
node2 = node2.next
return result

'AI HW study > 자료구조·알고리즘' 카테고리의 다른 글
| 05. 스택, 큐, 덱 - Stack (0) | 2023.08.16 |
|---|---|
| 03. 정렬 - 기수 정렬, 정렬 속도 비교, 병합 정렬, 퀵 정렬, 합 정렬, Stable Sort, In-place Sort (0) | 2023.08.14 |
| 03. 정렬 - Bubble Sort, 선택 정렬, 삽입 정렬 (0) | 2023.08.10 |
| 02 배열, 연결 리스트 - 이중 연결 리스트, Iterator, 원형 연결 리스트 (0) | 2023.08.08 |
| 01 시간, 공간복잡도 (0) | 2023.08.02 |



