< 격자 안에서 한 칸씩 이동하는 경우 >
다음과 같이 4개의 행으로 이루어진 직각삼각형 모양으로 된 판에 숫자들이 주어졌을 때, 최상단에서 시작하여 최하단으로 이동했을 때 얻을 수 있는 최대 합을 구해보려고 합니다.

단, 특정 위치 (r, c)에서의 이동은 (r+1, c) 혹은 (r+1, c+1) 지점으로만 가능합니다.
그렇다고 큰 숫자로만 따라 내려간다고 항상 더 좋은 값을 기대할 수는 없습니다. 예를 들어 다음 경우에는 우측처럼 아래로만 내려가는 것이 더 좋은 결과를 가져오게 됩니다.

이때 dp[i][j]를 마지막으로 방문한 위치를 (i, j)라 했을 때, 얻을 수 있는 최대 합이라 정의한다면 (i, j)에 도달하는 경우는 다음과 같이 2가지 경우를 생각해볼 수 있을 것입니다.
- (i, j)에 최종적으로 도달하기 위해서는 바로 위에서 내려오는 경우
- 좌측 모서리에서 내려오는 경우
2가지 밖에 없기 때문에 이 중 더 좋은 경우를 선택해주면 가장 좋은 답을 고를 수 있게 됩니다.

처음 주어진 다음 예시에 대해 DP 테이블을 채워보도록 하겠습니다.
먼저 시작점은 처음에 적혀있었던 값 그대로 입니다.
첫 번째 열에 해당하는 칸들은 전부 위에서 올 수 밖에 없으므로 위에서 내려오는 경우로 생각하여 순서대로 채워줍니다.
행과 열의 위치가 동일한 대각선에 대해서는 전부 대각선 방향으로 밖에 올 수 없으므로, 대각선 방향으로 내려오는 경우로 생각하여 순서대로 채워줍니다.
남은 칸들은 위에서 부터 순서대로 왼쪽 -> 오른쪽 방향으로 채워줍니다. 이때 다음 점화식을 이용해 채워줍니다.
dp[i][j]=max(dp[i−1][j]+a[i][j],dp[i−1][j−1]+a[i][j])
| DP | 1 | 2 | 3 | 4 |
| 1 | 4 | |||
| 2 | 10 | 6 | ||
| 3 | 13 | 17 | 15 | |
| 4 | 16 | 21 | 26 | 24 |
DP 테이블을 전부 채우고 나면, 가장 끝 행에 도달할 수 있는 경우 중 최대 합이 되는 경우를 선택해야 하므로 답은 26이 됩니다. 이런식으로 문제 상황에 맞는 적절한 점화식을 세우고 해당 점화식에 맞춰 DP 테이블에 값을 순서대로 채워넣으면 문제에서 원하는 답을 구할 수 있게 됩니다.
< 삼각형 >
다음과 같이 5개의 행으로 이루어진 직각삼각형 모양으로 된 판에 숫자들이 주어졌을 때, 최상단에서 시작하여 최하단으로 이동했을 때 얻을 수 있는 최대 합을 구해보려고 합니다.

맨 위층 12에서 시작하며, 특정 위치 (r, c)에서의 이동은 (r+1, c) 혹은 (r+1, c+1) 지점으로만 가능합니다.
이를 계산하기 위해 dp[i][j]를 마지막으로 방문한 위치를 (i, j)라 했을 때, 얻을 수 있는 최대 합이라 정의하여 dp table을 완성시켜보려고 합니다.
다음 빈칸에 들어갈 숫자를 순서대로 골라보세요.
| DP | 1 | 2 | 3 | 4 | 5 |
| 1 | 12 | ||||
| 2 | 22 | 23 | |||
| 3 | 35 | 35 | 34 | ||
| 4 | 43 | 42 | 45 | 45 | |
| 5 | 55 | 54 | 56 | 55 | 54 |
< 정수 사각형 >
다음과 같이 8 * 8 크기의 행렬이 주어졌을 때, (1, 1)에서 시작하여 오른쪽 혹은 밑으로만 이동하여 (8, 8)로 간다고 했을 때 거쳐간 위치에 적혀있는 숫자의 합 중 가능한 최댓값은 어떻게 될까요?
9 6 1 5 3 7 8 5
3 4 2 5 7 8 7 9
8 7 7 6 4 3 5 7
3 6 8 9 5 7 7 9
8 7 6 2 3 5 6 8
1 2 3 4 5 2 3 5
9 8 7 6 8 3 4 5
6 5 4 6 3 7 9 9
>>
| 9 | 15 | 16 | 21 | 24 | 31 | 39 | 44 |
| 12 | 19 | 21 | 26 | 33 | 41 | 48 | 57 |
| 20 | 27 | 34 | 40 | 44 | 47 | 53 | 64 |
| 23 | 33 | 42 | 51 | 56 | 63 | 70 | 79 |
| 31 | 40 | 48 | 53 | 59 | 68 | 76 | 87 |
| 32 | 42 | 51 | 57 | 64 | 70 | 79 | 92 |
| 41 | 50 | 58 | 64 | 72 | 75 | 83 | 97 |
| 47 | 55 | 62 | 70 | 75 | 82 | 92 | 106 |
< 조건에 맞게 선택적으로 전진하는 경우 >
다음과 같이 6개의 숫자가 주어졌을 때, 가장 긴 증가 부분 수열(LIS)의 길이를 구해보려고 합니다.
[10, 30, 25, 40, 28, 45]
여기서 부분수열이란 수열에서 일부 숫자를 선택해서 만든 또 다른 수열이며, 증가하는 부분수열이란 숫자가 점점 증가하는 부분수열을 의미합니다.
예를 들어, 10, 30, 25, 40, 28, 45 이라는 수열이 있다고 가정하면, 10, 30, 40 같은 수열은 증가하는 부분수열이지만
28, 40, 45는 순서대로 나오지 않으므로 부분수열이 아닙니다.
위의 예시에서 LIS는 10, 30, 40, 45입니다.
그렇다고 첫 번째 숫자를 시작으로 계속 증가하는 값만 고른다고 해서 항상 LIS가 구해진다고 할 수는 없습니다.
예를 들어 주어진 수열이 10, 30, 20, 22, 23, 24, 21인 경우, 10, 20, 22, 23, 24가 LIS가 됩니다.
이때 dp[i]를 마지막으로 고른 원소의 위치가 i인 부분 수열 중 최장 증가 부분 수열의 길이라 정의해보겠습니다.
그렇다면 수열 10, 30, 25, 40, 28, 45에 대해 다음과 같이 DP 배열에 값이 채워져야 합니다.
dp[1]값이 1인 이유는 원소 10으로 끝나는 LIS가 10이기 때문이고,
dp[2]값이 2인 이유는 원소 30으로 끝나는 LIS가 10, 30이기 때문이고,
dp[3]값이 2인 이유는 원소 25로 끝나는 LIS가 10, 25이기 때문입니다.
다른 예시로 20, 30, 10, 5, 50으로 이루어진 수열이라면, DP값이 다음과 같이 채워집니다.
dp[3]값이 1이 되는 이유는 정확히 10으로 끝나는 LIS가 10이기 때문입니다.
dp[i]의 정의가 정확히 i번째 원소를 끝으로 하는 LIS의 길이 이므로, dp[2]값이 2였다고 하더라도 dp[3]의 값은 1이 되어야만 합니다. 마찬가지 이유로 dp[4]값은 1이 됩니다.
또 다른 예시로 25, 5, 10, 30으로 이루어진 수열이라면, DP값이 다음과 같이 채워집니다.
dp[4]의 값이 3이 되는 이유는, 숫자 30보다 작은 숫자 중 dp값이 가장 큰 dp[3]에 1을 더해야 LIS가 되기 때문입니다.
이와 같이 수열을 이루고 있는 원소의 개수(N)가 적을 때는 직접 셀 수 있겠지만, N이 100인 경우만 해도 직접 계산하는 것은 불가능할 겁니다.
i번째 원소를 고르기 직전에 골라진 원소의 위치가 j였을 경우를 1부터 i - 1까지 전부 가정해보며 다음과 같은 점화식을 세워볼 수 있을 것입니다.
dp[j]는 위치 j를 마지막으로 하는 최장 부분 수열의 길이를 들고 있을 것이기 때문에, dp[i]는 dp[j]로부터 답이 갱신되어야만 합니다. 단, 직전에 있던 숫자 a[j]가 현재 숫자인 a[i]보다는 작아야 증가 수열이 유지가 될 것이므로, 해당 경우들 중 최댓값을 구해야 합니다.



< 가장 긴 증가하는 부분 수열 >
다음과 같이 10개의 숫자가 주어졌을 때, 가장 긴 증가 부분 수열(LIS)의 길이를 구해보려고 합니다.
[20, 80, 10, 50, 55, 20, 60, 70, 5, 90]
여기서 부분 수열이란 수열에서 일부 숫자를 선택해서 만든 또 다른 수열이며, 증가하는 부분 수열이란 숫자가 점점 증가하는 부분 수열을 의미합니다. 예를 들어, 10, 30, 25, 40, 28, 45 이라는 수열이 있다고 가정하면, 10, 30, 40 같은 수열은 증가하는 부분 수열이지만 28, 40, 45는 순서대로 나오지 않으므로 부분 수열이 아닙니다. 10, 30, 25, 40, 28, 45 수열에서의 LIS는 10, 30, 40, 45이 됩니다.
맨 위에 주어진 예시 수열에서의 LIS를 계산하기 위해 dp[i]를 마지막으로 고른 원소의 위치가 i인 부분 수열 중 최장 부분 수열의 길이라 정의하여 dp table을 완성시켜보려고 합니다.
다음 빈칸에 들어갈 숫자를 순서대로 골라보세요.
| DP | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| - | 1 | 2 | 1 | 2 | 3 | 2 | 4 | 5 | 1 | 6 |
< 가장 긴 감소하는 부분 수열 >
다음과 같이, 조금 긴 수열이 존재합니다. 이 수열에서 가장 긴 감소하는 부분수열의 길이는 몇이 될까요?
60 65 50 70 63 55 45 51 45 48 54 70 61
여기서 부분수열이란 수열에서 일부 숫자를 선택해서 만든 또 다른 수열이며, 감소하는 부분수열이란 숫자가 점점 감소하는 부분수열을 의미합니다.
예를 들어, 45, 50, 25, 10, 18, 20 이라는 수열이 있다고 가정하면, 45, 25, 10 같은 수열은 감소하는 부분수열이지만 50, 20, 10은 순서대로 나오지 않으므로 부분수열이 아닙니다. 45, 50, 25, 10, 18, 20 수열에서 가장 긴 감소하는 부분수열은 45, 25, 10이 됩니다.
가장 긴 감소하는 부분수열의 길이를 구해봅시다. >> 최댓값은 5
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 1 | 2 | 3 | 4 | 4 | 5 | 5 |
| 11 | 12 | 13 |
| 4 | 1 | 3 |
< 아이템을 적절히 골라야 하는 경우 >
가치가 1, 4, 5인 3개의 동전이 주어졌을 때, 금액 8을 거슬러 주기 위해 필요한 최소 동전의 수를 구해보려고 합니다.
무턱대고 가치가 큰 동전부터 거슬러주면 8 = 5 + 1 + 1 + 1이 되어 4개의 동전이 필요해지게 됩니다. 하지만 이 경우 가치가 4인 동전을 2개 써서 8을 만들 수 있으므로 필요한 최소 동전의 수는 2가 됩니다.
이때 dp[i]를 지금까지 선택한 동전의 합이 i라 했을 때, 필요한 최소 동전 횟수라고 정의해보겠습니다.
수가 적으면 직접 셀 수 있겠지만, 거슬러줘야 하는 금액이 100인 경우만 해도 직접 계산하는 것은 불가능할 겁니다.
그렇다면 점화식을 세워야겠죠.
조금 고민해보면 총 n개의 동전 중 합 i를 만들기 위해 마지막으로 가치가 coin[j]인 j번째 동전을 고른 경우를 전부 가정해보며 다음과 같은 점화식을 세워볼 수 있을 것입니다.
합 i를 만들어야 하기 때문에, 마지막으로 동전 coin[j]를 사용했다면 이전 동전들로 만들었어야 하는 합은 i-coin[j]일 것입니다. 따라서 dp[i]는 dp[i-coin[j]]에 동전 하나를 더 추가했으므로 1을 더한 값과 비교가 되어야 합니다. 단, i가 coin[j]보다 작다면 다음 경우는 불가능할 것이기 때문에 i가 coin[j]보다 같거나 큰 경우들 중 최솟값을 구해야 합니다.

처음 주어진 다음 예시에 대해 DP 테이블을 채워보도록 하겠습니다.
동전 종류 : 1, 4, 5
거슬러줘야 하는 금액 : 8
먼저 전부 비워져 있는 상태로 시작합니다. 이때, 합을 0 만드는 데 필요한 최소 동전의 수는 아무 동전도 사용하지 않은 경우이므로 0이 됩니다.


합 8이 되기 위해 다음 3가지 경우가 있을 수 있습니다.
- Case 1. 마지막으로 사용한 동전이 가치가 1인 동전이었을 경우 : 마지막으로 동전 1을 사용하여 합이 8이 되기 위해서는, 그 전까지의 합이 7이었어야 합니다. 따라서 dp[7]값인 3에 1을 더한 값인 4가 하나의 후보가 됩니다.
- Case 2. 마지막으로 사용한 동전이 가치가 4인 동전이었을 경우 : 마지막으로 동전 4을 사용하여 합이 8이 되기 위해서는, 그 전까지의 합이 4였어야 합니다. 따라서 dp[4]값인 1에 1을 더한 값인 2가 하나의 후보가 됩니다.
- Case 3. 마지막으로 사용한 동전이 가치가 5인 동전이었을 경우 : 마지막으로 동전 5를 사용하여 합이 8이 되기 위해서는, 그 전까지의 합이 3이었어야 합니다. 따라서 dp[3]값인 3에 1을 더한 값인 4가 하나의 후보가 됩니다.
최소 동전의 수를 계속 구해야 하므로, 이 3개의 후보 중 최솟값인 2가 dp[8]에 적히게 됩니다.
이렇게 DP 테이블을 전부 채우고 나면, 정확히 8 만큼 거슬러줘야 하므로 답은 dp[8]인 2가 됩니다.
이런식으로 문제 상황에 맞는 적절한 점화식을 세우고 해당 점화식에 맞춰 DP 테이블에 값을 순서대로 채워넣으면 문제에서 원하는 답을 구할 수 있게 됩니다.
< 은행 >
가치가 1, 4, 5, 9인 4개의 동전이 주어졌을 때, 금액 21을 거슬러 주기 위해 필요한 최소 동전의 수를 구해보려고 합니다.
이 문제를 해결하기 위해 dp[i]를 지금까지 선택한 동전의 합이 i라 했을 때, 필요한 최소 동전 횟수라고 정의하여 dp table을 완성시켜보려고 합니다.
다음 빈칸에 들어갈 숫자를 순서대로 골라보세요.


< Knapsack >
도둑이 보석방을 털러 갔습니다. 이때 도둑 가방의 크기는 8이며, 이보다 더 많은 양의 무게에 해당하는 보석들을 담아 나올 수는 없습니다. 또한, 보석은 종류별로 단 하나씩만 있습니다.
이 도둑방에 있는 보석의 무게와 가격은 다음과 같습니다.
| 보석 번호 | 무게 | 가격 |
| 1 | 2 | 3 |
| 2 | 6 | 5 |
| 3 | 2 | 4 |
| 4 | 3 | 2 |
| 5 | 4 | 3 |
이러한 문제의 경우 무게가 가벼운 것 부터 담았을 때가 최적이지 않은 경우도 있고, 가격이 높은 것 부터 담았을 때 역시 최적이 아닌 경우가 있습니다.
이 문제를 해결하기 위해 동적계획법을 사용해보려고 합니다.
dp[i][j]를 i번째 보석까지 고려했고, 지금까지 선택한 보석 무게의 합이 총 j였을 때, 가능한 보석 가치의 최대 합이라고 정의해보겠습니다. 그렇다면 위 예시에 대해서는 다음과 같이 DP table 값이 채워져야 합니다.
dp[2][6] 값은 1번째 보석부터 2번째 보석까지만을 이용하여, 고른 보석 무게의 합이 정확히 6이 되는 경우 중 얻을 수 있는 최대 가치를 의미합니다. 이게 가능한 경우는 2번 보석 하나만 가방에 넣었을 경우이므로, 2번 보석의 가치인 5가 됩니다.
dp[2][8] 값은 1번째 보석부터 2번째 보석까지만을 이용하여, 고른 보석 무게의 합이 정확히 8이 되는 경우 중 얻을 수 있는 최대 가치를 의미합니다. 이게 가능한 경우는 1번, 2번 보석 모두를 골랐을 경우이므로, 1번, 2번 보석의 가치의 합인 8이 됩니다.
더 나아가 dp[5][6] 값은 1번째 보석부터 5번째 보석까지 전부 이용하여, 고른 보석 무게의 합이 정확히 6이 되는 경우 중 얻을 수 있는 최대 가치를 의미합니다. 이는 보석 2만 골랐을 경우에도 가능하지만 이때의 가치는 5이고, 보석3과 보석5 이렇게 2개를 골랐을 경우에는 가치의 합이 7이 되기 때문에 dp[5][6] 값은 7이 됩니다.
수가 적으면 이렇게 직접 셀 수 있겠지만, 보석의 수가 많아지면 직접 계산하는 것이 불가능할 것입니다.
그렇다면 점화식을 세워야겠죠. 조금 고민해보면 결국 i번째 보석까지 고민한 경우이므로 i번째 보석을 가방에 넣었는지/넣지 않았는지 여부로 나눠 점화식을 세워볼 수 있을 것입니다.
- i번째 보석을 가방에 넣은 경우
- dp[i][j]의 정의상 보석 무게의 합을 j로 만들어야 하기 때문에, i번째 보석을 가방에 넣은 경우라면, i-1번째까지 골라진 보석 무게의 합은 j-weight[i]가 될 것입니다. 이 경우라면 이전에 선택한 보석들로부터 얻을 수 있는 최대 가치인 dp[i-1][j-weight[i]]에 현재 i번째 보석을 가방에 넣으므로서 새로 얻게된 가치인 value[i]를 더하여 dp[i-1][j-weight[i]] + value[i]라는 가치를 얻게 될 것입니다. 다만 이 경우에는 j가 weight[i]보다 같거나 커야지만 말이 되므로, 이러한 경우에만 고려가 가능합니다.
- i번째 보석을 가방에 넣지 않은 경우.
- dp[i][j]의 정의상 보석 무게의 합을 j로 만들어야 하지만, i번째 보석을 선택하지는 않았으므로 i-1번째까지 골라진 보석 무게의 합이 정확히 j가 되어야 합니다. 따라서 이때 얻을 수 있는 최대 가치는 dp[i-1][j]가 됩니다.
따라서 점화식은 2가지 경우 중 더 큰 가치를 얻을 수 있는 쪽을 선택해주는 식으로 정의가 됩니다.

먼저 전부 비워져 있는 상태로 시작합니다.
1번째 보석의 경우, 가방에 담지 않는다면 무게 0, 가치도 0이므로 dp[1][0]값은 0이 되며, 가방에 담는다면 무게 2에 가치는 3이 되므로 dp[1][2]는 3이 됩니다.
그 이후부터는 다음과 같이 채워야 합니다.
예를 들어 다음과 같이 채워져 있을 때 dp[3][8]에 들어가야 할 값을 어떻게 계산하는 지에 대해 알아보겠습니다.

3번째 보석의 무게는 2, 가격은 4입니다.
먼저 3번째 보석을 사용하여 무게를 8을 만든다고 생각해보겠습니다. 그렇다면 2번째 보석까지는 정확히 무게 6을 이용해 최대 가치를 얻었어야 합니다. 여기에 3번째 보석을 넣게 되어 추가적으로 가치 4만큼을 더 얻게 되는 것이죠. 따라서 이 경우에 얻을 수 있는 가치는 dp[2][6] + 4가 됩니다.

만약 3번째 보석을 사용하지 않고 무게를 8을 만들었다고 생각해보겠습니다. 그렇다면 2번째 보석까지는 정확히 무게 8을 이용해 최대 가치를 얻었어야 합니다. 따라서 이 경우에 얻을 수 있는 가치는 dp[2][8]이 됩니다.

즉, dp[3][8]은 dp[2][6] + 4와 dp[2][8]중 최댓값을 골라야 하므로 5+4와 8중 더 큰 값인 9가 들어가게 됩니다.
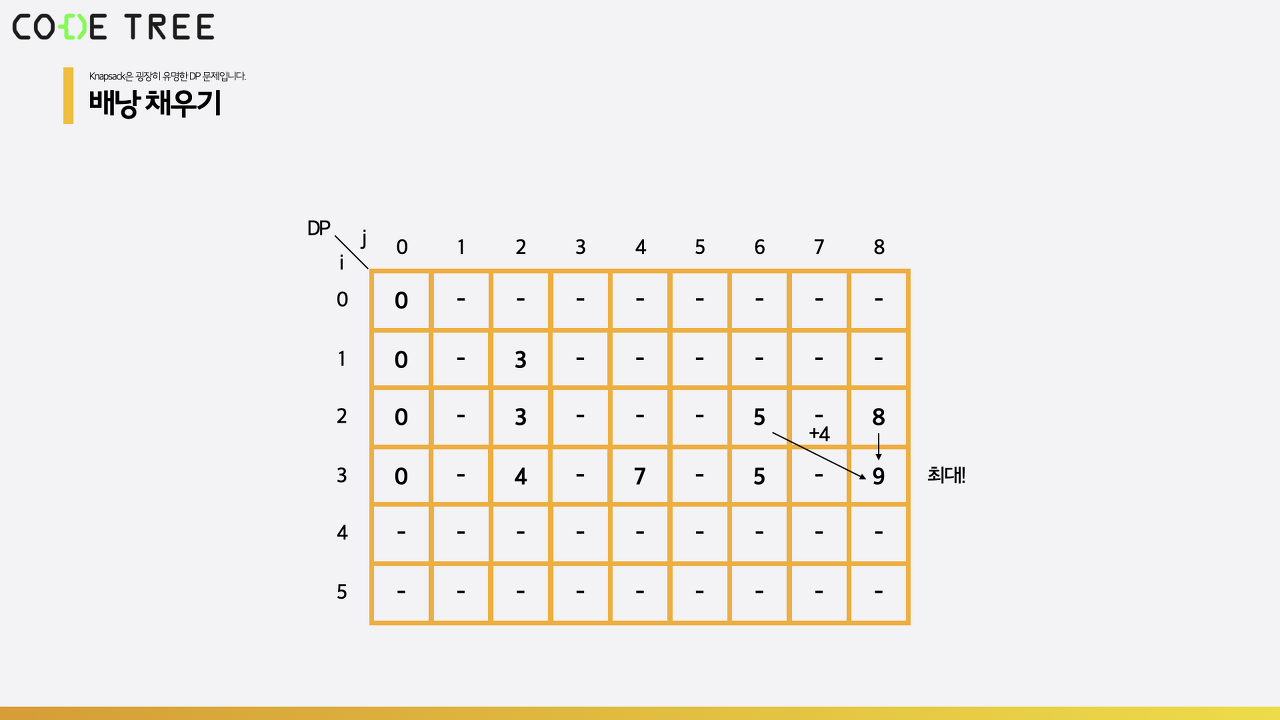
이런식으로 모든 숫자들을 순차적으로 채우게 되면 다음과 같은 결과를 얻을 수 있게 됩니다.
| DP | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 0 | - | 3 | - | - | - | - | - | - |
| 2 | 0 | - | 3 | - | - | - | 5 | - | 8 |
| 3 | 0 | - | 4 | - | 7 | - | 5 | - | 9 |
| 4 | 0 | - | 4 | 2 | 7 | 6 | 5 | 9 | 9 |
| 5 | 0 | - | 4 | 2 | 7 | 6 | 7 | 9 | 10 |
<유사 문제 1 >
| 보석 번호 | 무게 | 가격 |
| 1 | 3 | 4 |
| 2 | 1 | 1 |
| 3 | 4 | 2 |
| 4 | 5 | 6 |
| 5 | 2 | 3 |
이를 계산하기 위해 dp[i][j]를 i번째 보석까지 고려했고, 지금까지 선택한 보석 무게의 합이 총 j였을 때, 가능한 보석 가치의 최대 합이라고 정의하여 dp table을 완성시켜보려고 합니다. 다음 빈칸에 들어갈 숫자를 순서대로 골라보세요.
| DP | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 0 | - | - | 4 | - | - | - | - | - |
| 2 | 0 | 1 | - | 4 | 5 | - | - | - | - |
| 3 | 0 | 1 | - | 4 | 5 | 3 | - | 6 | 7 |
| 4 | 0 | 1 | - | 4 | 5 | 6 | 7 | 6 | 10 |
| 5 | 0 | 1 | 3 | 4 | 5 | 7 | 8 | 9 | 10 |


< 유사 문제 2 >
도둑이 보석방을 털러 갔습니다.
이때 도둑 가방의 크기는 20이며, 이보다 더 많은 양의 무게에 해당하는 보석들을 담아 나올 수는 없습니다.
또한, 보석은 종류별로 단 하나씩만 있습니다.
이 도둑방에 있는 보석의 무게와 가격은 다음과 같습니다.
| 보석 번호 | 무게 | 가격 |
| 1 | 2 | 3 |
| 2 | 6 | 5 |
| 3 | 2 | 4 |
| 4 | 3 | 2 |
| 5 | 4 | 3 |
| 6 | 5 | 3 |
| 7 | 4 | 2 |
| 8 | 6 | 6 |
| 9 | 7 | 9 |
| 10 | 10 | 8 |
이를 계산하기 위해 dp[i][j]를 i번째 보석까지 고려했고, 지금까지 선택한 보석 무게의 합이 총 j였을 때, 가능한 보석 가치의 최대 합이라고 정의하여 dp table을 완성시켜보려고 합니다.
다음 빈칸에 들어갈 숫자를 순서대로 골라보세요.

(1) 15 (2) 17 (3) 13 (4) 24 (5) 18
< 숫자 암호 만들기 > ???
숫자를 쪼개서 암호처럼 사용하려고 합니다. 암호를 만드는 과정은 다음과 같습니다.
1. 숫자를 1, 2, 3, 4의 합으로 바꿉니다.
2. 숫자의 합에서 사용된 숫자를 일렬로 나열합니다.
예를 들어, 4를 활용하면
1 + 1 + 1 + 1 → 1111
1 + 1 + 2 → 112
1 + 2 + 1 → 121
2 + 1 + 1 → 211
1 + 3 → 13
2 + 2 → 22
3 + 1 → 31
4 → 4
와 같이 8개의 암호를 만들 수 있습니다.
이런 방식으로 암호를 만든다고 가정하면, 8 로는 몇 개의 암호를 만들 수 있을까요?
Hint
동전 거슬러주는 문제에서의 풀이와 비슷한 방식으로 접근하면 됩니다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 2 | 4 | 8 | 15 | 29 | 56 | 108 |





'AI HW study > 자료구조·알고리즘' 카테고리의 다른 글
| 04. 이진탐색 - 이진탐색, 순차탐색, lower/Upper Bound (0) | 2023.08.24 |
|---|---|
| 08. DP - String Matching, Greedy 알고리즘 (0) | 2023.08.20 |
| 08. DP - 동적계획법, Memoization, Tabulation, subproblem을 그대로 합치면 되는 DP (0) | 2023.08.20 |
| 07. 해싱 (0) | 2023.08.20 |
| 06. 트리 - Heap (0) | 2023.08.18 |


